Ученые не могут решить простую математическую задачу уже больше 80 лет

«Итак, Нобелевскую премию за доказательство Гипотезы Коллатца получает...» Ого, называют ваше имя! Все встают и аплодируют герою этого дня. В вашу честь запускают салют. Он такой громкий, что вы просыпаетесь посреди урока математики. Оказывается, нет никакой Нобелевской премии по математике, ведь никто, включая вас, до сих пор не смог доказать ту гипотезу. Вот в чем ее суть. Выберите число от одного до девяти. Давайте возьмем пять. Поскольку это число нечетное, мы умножим его на три и добавим один. Итак, пятнадцать плюс один равно шестнадцать. Это число четное, поэтому мы делим его на два. Ту же схему мы будем применять к каждому последующему полученному числу.

Шестнадцать, поделенное на два, дает восемь. Итак, если восемь разделить на два, будет четыре. Четыре, разделенное на два, дает два. Два, разделенное на два, один. Все просто, да? Один — нечетное число, поэтому умножаем его на три и добавляем единицу. И снова получаем четыре. Четыре, разделенное на два, дает два, два, разделенное на два, один. Мы можем продолжать до бесконечности и в итоге всякий раз получать один. Мы застряли в этом цикле. Кроме того, мы не можем предсказать природу цикла. Он может быть коротким, как этот, а может длинным. Но в любом случае, он приведет нас к единице. Интересно, что математики не могут доказать существование числа, способного разорвать этот цикл и не привести к единице. Возможно, есть некое огромное число, которые не застревает в этой петле и не приводит к одному или стремится к бесконечности.

Гипотеза Коллатца, также известная как дилемма три эн плюс один, была названа в честь доктора Лотара Коллатца. Он посвятил много времени и исследований доказательству этой гипотезы. Простая на первый взгляд теория уже восемьдесят лет приводит в затруднение светлые умы. Говорят, что она все еще непостижима для современной математики. Те, кто пытался ее доказать, советуют молодым математикам не тратить время. Но, если хотите попробовать, начинайте примерно с трехсот квинтиллионов. Все те, кто пытался сделать это до вас, уже проверили все меньшие числа.

Если вы хоть раз перевозили диван в новую квартиру, то вам знакома еще одна известная нерешенная задача. В коридоре есть поворот, и вам надо понять, как пронести через него диван. С маленьким диваном будет проще, а вот с большим!.. Да, он застрянет. Насколько большим может быть диван, чтобы обойти угол? Наибольшая площадь, проводимая за угол коридора, в этой задаче называется «константа дивана». Угол поворота девяносто градусов, где один означает ширину коридора. Суть проблемы состоит в двух измерениях. Математики до сих пор не могут назвать размеры самого большого дивана, способного протиснуться в поворот. Диван может быть любой формы, речь не только о прямоугольных. Некоторые оказываются слишком большими, другие свободно входят в поворот. Константа дивана находится где-то между двумя этими значениями.

Гипотеза о простых числах-близнецах настолько простая, что ее поймет каждый, но даже лучшие ученые мира не могут ее доказать. Итак, простое число — это любое число больше одного, которое делится только на один и на само себя. Составляя список простых чисел, можно заметить две вещи. Во-первых, чем дальше, тем чисел становится меньше. Они составляют двадцать пять процентов всех чисел от одного до ста, но всего пять от одного до миллиарда. Во-вторых, есть огромное количество так называемых чисел-близнецов. Это пары простых чисел, отличающихся на два. Три и пять, пять и семь, одиннадцать и тринадцать — всё это числа близнецы. Вопрос в том, закончатся ли они когда-нибудь?

Более двух тысяч трехсот лет назад известный греческий математик Евклид доказал, что простых чисел бесконечное множество. Возможно, как и чисел-близнецов. Однако, пока что это еще не доказано. Проверим, как хорошо вы помните свои уроки математики. Вам это о чем-нибудь говорит? Три буквы обозначают три стороны правильного треугольника. Все стороны пифагорова треугольника выражаются целыми числами. Если мы сделаем его трехмерным, то у нас будет четыре числа. В нашем примере это эй, би, си и джи. Эй, би и си — это стороны параллелепипеда, а джи — это диагональ, тянущаяся из этого верхнего угла к противоположному нижнему.

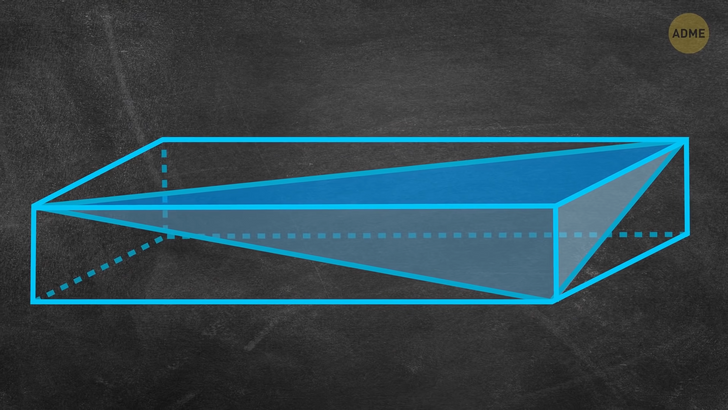
В некоторых случаях все три стороны и диагональ — это целые числа. А что насчет остальных трех диагоналей на трех других поверхностях: ди, и и эф? Могут ли все семь чисел быть целыми? Математики пытаются в этом разобраться и найти идеальный прямоугольный параллелепипед, но пока безуспешно. Они также не могут доказать, что его не существует. Поиски продолжаются.

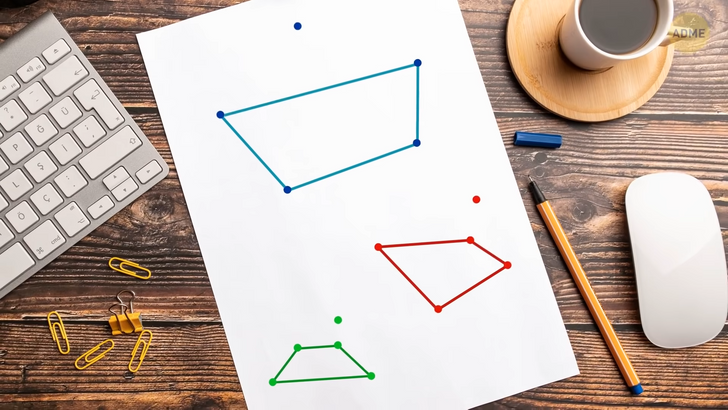
Задача со счастливым концом получила свое название после того, чем обернулась работа над ней двух математиков. Они поженились, но задачу так и не решили. Нарисуйте на листе бумаги пять точек в любом порядке. Я поставлю одну здесь, одну здесь и еще одну. Готово. Теперь давайте попытаемся соединить четыре из этих точек так, чтобы у нас получилась четырехсторонняя фигура, все углы которой меньше ста восьмидесяти градусов. Получилось! Переставим точки и попробуем еще раз. Да, снова сработало! Выходит, как бы вы ни располагали точки, вы всегда сможете нарисовать такую фигуру.

Но что, если сторон будет больше чем четыре? Ученые доказали, что для пятиугольника, пятисторонней фигуры, понадобится девять точек; а для шестиугольника — семнадцать. Что касается более крупных фигур, никто не знает точное количество точек или формулу для расчета этого количества для различных фигур. В общем, если хотите решить одну из перечисленных задач, надо как следует тренировать мозг. Начнем с простого задания для разминки.

Если один равно четырем, два равно трем, три равно трем, четыре — шести, а пять — четырем, то чему равно шесть? Единственное, что вам здесь надо посчитать, так это количество букв в каждой цифре. Правильный ответ пять, потому что именно столько букв в слове «шесть».

Художник работает над инсталляцией, погружая тарелки в воду. Каждый день число тарелок увеличивается вдвое. Итак, если художнику требуется сорок восемь дней, чтобы покрыть все озеро тарелками, то сколько ему потребуется, чтобы покрыть половину озера? Двадцать четыре дня — неверный ответ! Правильный ответ: сорок семь! Поскольку размер инсталляции удваивается каждый день, то половину озера она покроет за день до того, как покроет его целиком.

Эта машина скрывает один номер парковочного места. Можете его назвать? В Гонконге эту математическую задачу тестировали на шестилетках! Итак, у вас уже есть ответ? Нужно просто перевернуть картинку вверх ногами, чтобы узнать, что правильный ответ — восемьдесят семь.

А вот задача посложнее. Вы поднимаетесь на гору. Она имеет наклон. Расстояние до вершины — сто шестьдесят километров. Каждый день вы продвигаетесь на три километра. Но во время ночного отдыха скатываетесь на километр шестьсот метров вниз, так как гора имеет наклон. Сколько дней вам потребуется, чтобы добраться до вершины и установить там флаг? Правильный ответ: девяносто девять дней. Вы будете проходить по три километра каждый день, вычитая потерянное за ночь расстояние. Выходит, ежедневный прогресс будет составлять километр шестьсот метров. Вы преодолеете дистанцию в сто пятьдесят семь километров за девяносто восемь дней, а затем пройдете оставшиеся три километра на девяносто девятый.

Это уравнение не имеет никакого смысла. Но если вы нарисуете всего одну линию в нужном месте, то уравнение будет полностью точным. Итак, где должна проходить эта линия? Ее нужно провести на любом из плюсов. Теперь все абсолютно логично! Есть три цифры. Неважно, будете вы их складывать или умножать, ответ будет одинаковым. Что это за цифры? Это цифры один, два и три.