"Санта никогда не бреется, поэтому второй багаж выглядит подозрительно: в нем есть крем для бритья."
Ой, всё
13 загадок, которые заставят вас сомневаться в реальности
Китти руководит танцевальным шоу. Она приехала в Финляндию с тремя лучшими танцорами, чтобы выступить во время зимних праздников. В первый день поездки Китти была найдена без сознания в гостиничном номере. Врачи утверждают, что ее кто-то отравил. Полиция допрашивает всех танцоров. Кира рассказывает: «Мы с коллегами покинули отель рано утром, чтобы осмотреть город. А Китти осталась в номере из-за онлайн-звонка. Ей звонил ее парень — Майкл». Пэм говорит: «Я пошла на пляж, чтобы позагорать и поплавать. Когда я вернулась, я увидела Китти на полу». А Эйприл говорит: «Я пошла в музей одна. Никто не захотел составить мне компанию». Кто лжет?

Пэм. Сейчас зимние каникулы, и в Финляндии холодно. Она не могла купаться и загорать.

Полиция арестовала Пэм. Кире и Эйприл срочно нужно найти новую танцовщицу для своего шоу. Они просматривают анкеты в Интернете и видят три интересные кандидатуры: Дебру, Салли и Лили. Но только один из профилей настоящий. Сможете сказать который?

Профиль Дебры выглядит хорошо. Но присмотритесь к тени на ее фотографии. Ее голова прифотошоплена к телу другого человека. Она не та, за кого себя выдает. А согласно дате рождения третьей девушки, она еще не родилась. Поэтому в команду стоит взять Салли.

Эйприл, Кира и Салли выступают в мюзик-холле. Но сначала они идут в гримерку, чтобы подготовиться. Вдруг заходит местный охранник и объявляет: «Стойте на месте! Мы должны перепроверить весь багаж. Среди артистов есть сбежавший преступник». Вот багаж, который оставили три парня, играющие Санту. Можете понять, кто преступник?
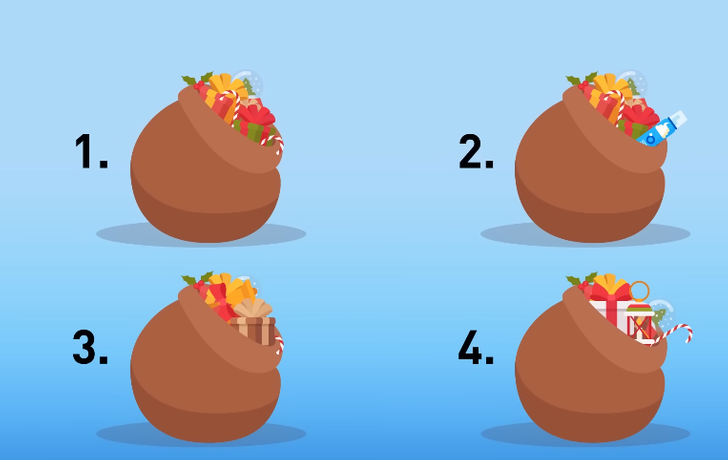
Санта никогда не бреется, поэтому второй багаж выглядит подозрительно: в нем есть крем для бритья.

Оставшиеся три Санты открывают представление. В своих костюмах они выглядят абсолютно одинаково. После представления они уходят за кулисы, снимают бороды и шапки, чтобы выпить кофе. Это Карл, Питер и Джордж.

После перерыва они снова надевают костюмы и отправляются на вечеринку. Можете догадаться, кто из них Карл?

Карл размешивал сахар в кофе левой рукой. Значит, он левша. А этот Санта дает автограф левой рукой. Следовательно, он — Карл.

После работы Кира и Эйприл идут на местный парад. Можете помочь им найти овечку среди всех этих Сант?

Вот она.

А что насчет этих оленей? Видите среди них медведей?

Привет!

Кира и Эйприл заходят в торговый центр и сталкиваются с четырьмя Сантами, покупающими подарки для своих семей. Тем временем охранник торгового центра получает звонок из полиции. Таинственный вор в костюме Санты ограбил несколько магазинов подарков. В полиции выяснили, что этот торговый центр должен стать следующим.
Охранник просит всех оставаться на местах. Можете помочь ему найти преступника?

Это третий Санта. Он прячет в своем мешке монтировку. Кроме того, его борода и усы отличаются от бород и усов других Сант.

Кира и Эйприл решают устроить вечеринку в номере отеля. Эйприл украшает комнату и устанавливает елку. Тем временем Кира готовит ужин и упаковывает подарки для трех человек: Томаса, Салли и Майкла. Гости прибывают, и вечеринка начинается. В какой-то момент девушки замечают, что кто-то украл все подарки. Кира считает, что это был кто-то из гостей. Поэтому она их расспрашивает. Каждый гость делает два заявления: одно правдивое и одно лживое.
Томас говорит: «Меня не было в комнате, когда это случилось. Я знаю, Майкл украл подарки». Салли говорит: «Майкл украл их, я видела. У меня и так достаточно подарков». И, наконец, Майкл говорит: «Я не крал подарки. Томас говорит правду — его не было в комнате». Кто украл рождественские подарки?

Если Томас — вор, то оба его утверждения были бы ложными. А если вор Майкл, то все утверждения Томаса были бы истинными. Следовательно, подарки украла Салли.

Фрэнк живет в гостиничном номере по соседству с Кирой. За день до Рождества она стучится к нему в дверь, чтобы одолжить зубную пасту. Дверь открыта, и Фрэнк лежит без сознания на полу. Позже в тот же день врачи выясняют, что он был отравлен. Кира расспрашивает трех человек.
Все они живут в одном номере с Фрэнком. Джефф говорит: «Сегодня я ужинал со своей девушкой. Я видел Фрэнка только утром, и он чувствовал себя отлично». Томас говорит: «Сегодня утром мы завтракали с Фрэнком в его комнате. Он был в отличном настроении». И Элли говорит: «Я только что вернулась. Мне нужно было купить подарки для родственников, поэтому я весь день ходила по магазинам». Кто отравил Фрэнка?

Видите подсказку на экране компьютера? Фрэнк зашифровал имя своего отравителя. Это был Томас.

Кира, Эйприл, Майкл и Фрэнк снимают уютный загородный дом, чтобы отпраздновать Рождество. Эйприл печет пряничных человечков и оставляет их остывать на кухонном столе. Она еще не нанесла глазурь, поэтому просит других держаться подальше от выпечки. Эйприл поднимается на второй этаж, чтобы переодеться.
Через десять минут она возвращается и видит, что кто-то откусил по кусочку от каждого пряника. Эйприл приходит в ярость. Она спрашивает всех: «Что вы делали в последние десять минут?» Майкл отвечает: «Я лепил снеговика на улице. Я понятия не имею, что происходило в доме». Фрэнк говорит: «Я украшал елку этими шариками». А Кира отвечает: «Я смотрела свой любимый сериал в спальне. Я включила его довольно громко и ничего не слышала». Эйприл уже знает, кто лжет. А вы?

Фрэнк лжет. На елке нет шариков.

Санта возвращается домой раньше времени и застает своего эльфа Бобби на диване. Он заколдован заклинанием вечного сна. Санта задает вопрос другому эльфу — Чаку: «Что здесь произошло? Дома были только вы двое!» Чак отвечает: «Мы упаковывали подарки и решили устроить перерыв на обед. Вдруг я услышал громкие звуки на улице и выбежал посмотреть, в чем дело. Я провел там около двадцати минут. Потом я вернулся домой. Бобби уже был заколдован». Санта называет Чака лжецом. Почему?

Чак сказал, что провел на улице двадцать минут, но кофе в чашках всё еще горячий. Чак заколдовал Бобби и пытается это скрыть.

Кира возвращается домой к семье. Ей не терпится съесть ореховое печенье, которое она купила в аэропорту. Ей придется есть его на улице, потому что у ее матери аллергия на все виды орехов. Через некоторое время Кира заглядывает в сумку и видит, что печенье исчезло. Кира подозревает своих братьев. Она спрашивает: «Кто съел мое печенье?!»
Дилан отвечает: «Я помогал маме готовить яблочный пирог». Пол говорит: «Я украшал гостиную». Кевин говорит: «Я делал бутерброд с арахисовым маслом для мамы». А Ральф говорит: "Я просто смотрел телевизор и ел попкорн".Теперь Кира знает, кто забрал ее печенье. А как насчет вас?

Кевин лжет. У них одна мать. И, как мы уже говорили, у нее аллергия на все виды орехов.

Во время семейного ужина Дилан получает электронное письмо и начинает плакать. Кира спрашивает: «Что случилось?» Дилан отвечает: «Я начинающий фотограф. И я отправил свое лучшее фото на конкурс. Я рассчитывал выиграть приз. Но меня дисквалифицировали!» Можете понять, почему, взглянув на эту фотографию?

Звезды расположены на фоне Луны. Это невозможно.
Комментарии
>> Оставшиеся три Санты...
Ой, все (2)
Преступная жизнь в Финляндии
Авторский ответ на логическую задачу о краже подарков совершенно не верен, а решение не представлено.
Так решим же её сами.
Вначале для краткости обозначим высказывания по авторству и очерёдности Т1, Т2, С1, С2, М1 и М2, истинные высказывания =1, ложные =0.
Помним, что если Т1=1, то Т2=0 и наоборот.
Т1: Томаса в комнате в момент кражи не было;
Т2: Томас знает, что вор — Майкл;
М1: вор — не Майкл;
М2=Т1;
С1: Майкл — вор;
С2: У Салли достаточно подарков. Высказывание-пустышка, ни на что не влияет.
1. Опровергаем вывод авторов.
Если вор — Салли, тогда С1=0, тогда М1=1, тогда М2=Т1=0, тогда Т2=1.
Противоречие. Следовательно, Салли — не вор, и авторы не правы.
2. Решение.
Поскольку Т1=М2, то Т2 и М1 также имеют одинаковые значения.
Если Т2=М1=1, то, действительно, имеется противоречие.
Но если Т2=М1=0, то никакаго противоречия нет.
М1=0 означает, что Майкл — вор, а Т2=0 означает не то, что Майкл — не вор, а то, что Томас НЕ ЗНАЕТ, кто вор.
Итак, вор — Майкл.
Похожее
Толковый текст о том, что хамов всегда следует ставить на место

10 стереотипов в отношении мужчин и женщин, мешают людям жить в удовольствие

16 иллюстраций о том, что для родителей современное поколение словно с луны спустилось

16 учителей, которые подпортили людям воспоминания о школьных годах

20 историй о людях, которых ослепила зависть

20+ человек, которые купили обычную вещь, а в ней обнаружился приятный сюрприз

19 странных вещей из мира моды, за которые многие люди готовы отдать любые деньги

20+ человек, которые вышли из магазина с полными пакетами впечатлений

15 историй о том, что даже вопрос выбора еды может подпортить отношения

15+ человек, которые начали ремонт и поняли, что скучать не придется

15 человек, которые лично убедились, что с ипотекой не соскучишься

17 историй о том, как люди реагировали на наглость и хамство
