18 человек, которым достались такие родственнички, что не позавидуешь

Пит Мондриан — нидерландский художник, который заложил начало абстрактной живописи наряду с Кандинским и Малевичем. В своих работах он использовал разноцветные прямоугольники разных площадей. Вдохновившись его картинами, математики придумали логическую задачку.
Сегодня ADME предлагает вам необычную головоломку, в которой идеально сочетаются геометрия и необходимость пораскинуть мозгами.
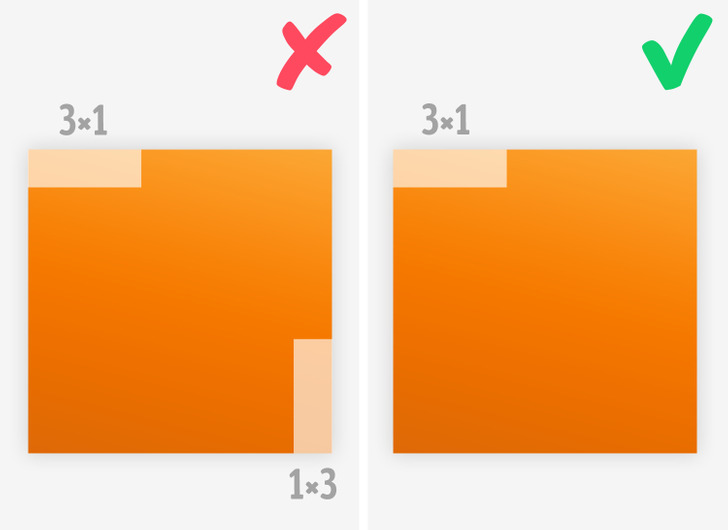
ЗАДАЧА:
ПОДСЧЕТ ОЧКОВ:

Для тренировки начнем с простого. Возьмем квадрат 4×4. Мы не можем разделить его пополам, так как это были бы одинаковые прямоугольники, а нам нужны уникальные. Сделаем, например, 4×3 и 4×1. Теперь подсчитаем наши очки:
4×3 — 4×1 = 12 — 4 = 8
Многовато. Попробуем улучшить результат с более сложным квадратом 8×8. Дальше мы будем работать с ним.

Начнем с того, что тоже разделим квадрат примерно пополам. Получаем:
5×8 — 3×8 = 40 — 24 = 16
Улучшим наш результат. Для этого разобьем большой прямоугольник слева еще раз.

5×5 — 3×5 = 25 — 15 = 10
Уже лучше. Но если просто продолжить разбивать большой прямоугольник на меньшие, то мы будем получать все меньшие и меньшие площади. Это будет увеличивать разницу между самым большим и самым маленьким, а значит, ухудшать результат. Так что же можно сделать?

Чтобы найти идеальное решение, запишем все возможные варианты площадей для этого квадрата. При этом мы не можем брать прямоугольники, где хотя бы одна сторона больше 8, так как такой квадрат просто не поместится внутрь.
В нашей таблице для примера приведены площади до значения 20 (хотя можно продолжать до 64).
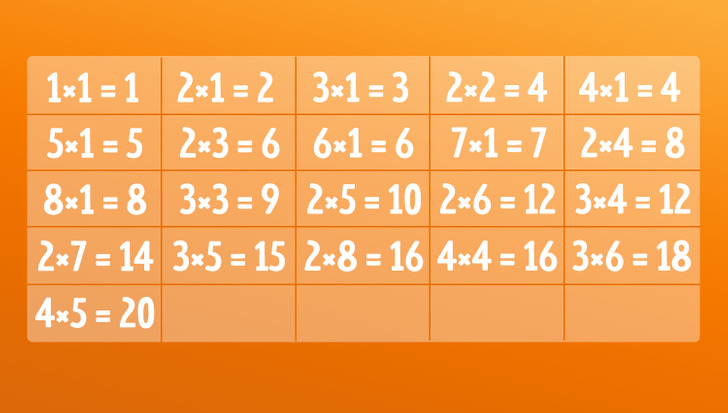
Если мы используем прямоугольник с нечетным значением площади, то нужно использовать еще один с нечетным, чтобы сумма получилась четной. Такие пары сложно подобрать, и к тому же они тоже увеличат наш результат. Поэтому все нечетные значения мы будем исключать. К примеру, 3×1 и 3×15 нам не подойдут.
Начнем с прямоугольника 2×7 = 14 и расположим его, например, с левой стороны. Он дает нам внизу пустое место со стороной всего 1. Чтобы найти для него подходящий вариант, нужно продолжить искать среди прямоугольников поменьше. Ищем нужные в нашей таблице.
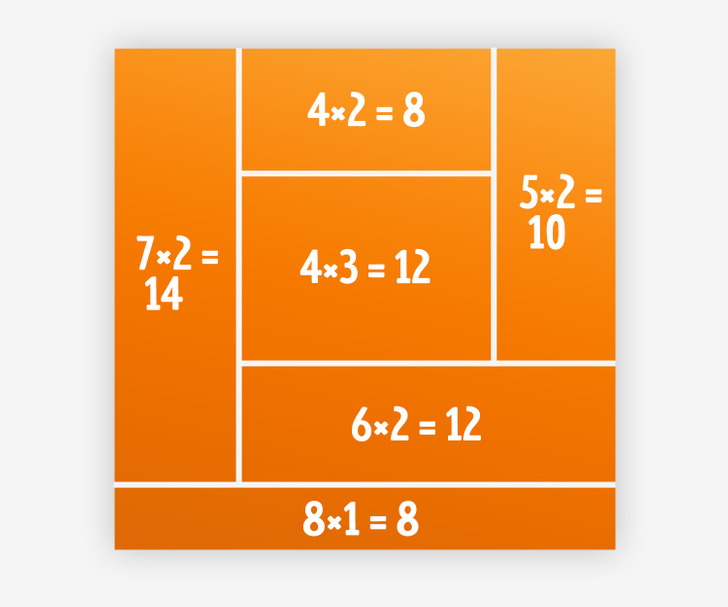
Итак, мы получили квадрат, заполненный 6 уникальными прямоугольниками. Считаем очки:
14 — 8 = 6
Результат 6 нельзя улучшить. Но его можно получить, подобрав другую комбинацию прямоугольников из нашей таблицы. Сможете ее найти?
Интересно, сможете ли вы найти решение этой задачки, используя квадрат 10×10 или даже 32×32? Даже математики не уверены, что это под силу кому-либо.