Если у вас все плохо с математикой — это не ваша вина. Нас просто не научили в школе математическим трюкам, с которыми любые расчеты становятся элементарными.
ADME публикует приемы, благодаря которым вы легко сможете считать в уме.
Процент от числа
Быстрое возведение в квадрат
Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5. Умножьте первую цифру саму на себя + 1, а в конце допишите 25. Вот и все!
Умножение на 9
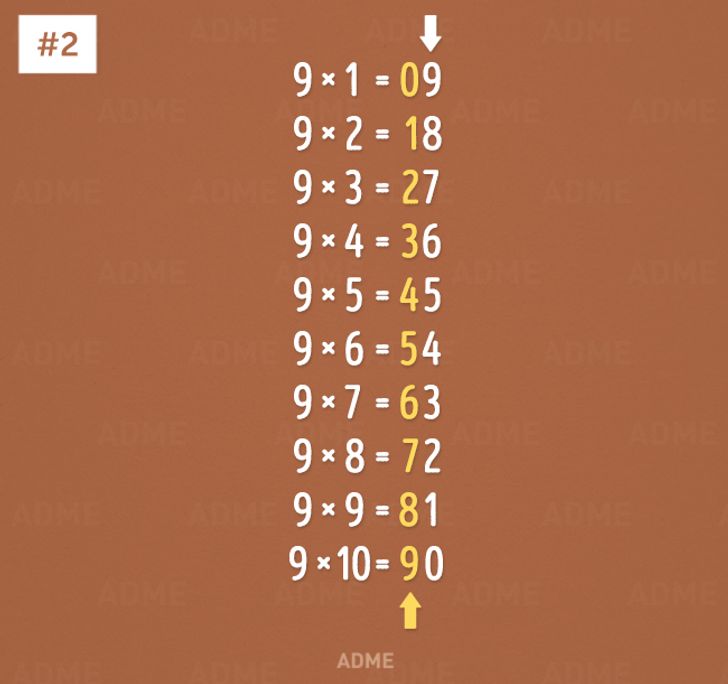
Умножение на 5
Разделите число на 2. Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5.
Умножение на 11
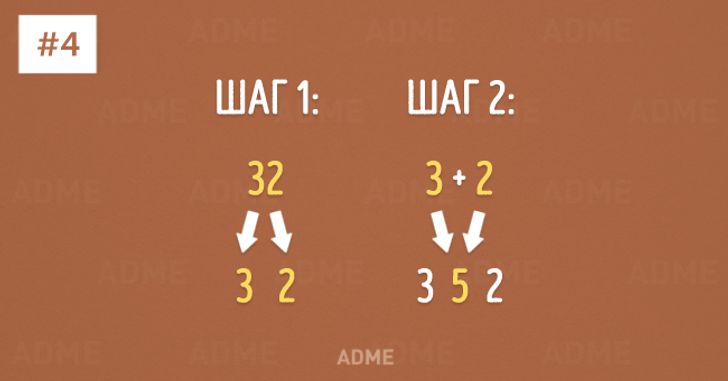
Умножение на 4
Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2.
Подсчет чаевых
Если вам нужно оставить 15% чаевых, есть простой способ определить, сколько это. Высчитайте 10% (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ.
Сложное умножение
Если вам нужно умножить большие числа, причем одно из них — четное, вы можете просто перегруппировать их, чтобы получить ответ.
Деление на 5
На самом деле делить большие числа на 5 очень просто. Все, что нужно, — это просто умножить на 2 и перенести запятую.
Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: отнимите от 9 все цифры, кроме последней, а последнюю цифру отнимите от 10.
Перевод градусов по Цельсию в градусы по Фаренгейту и наоборот
Быстрые кубические корни
Для того чтобы быстро считать кубический корень из любого числа, понадобится запомнить кубы чисел от 1 до 10:
Как только вы запомните эти значения, находить кубический корень из любого числа будет элементарно просто.
Пример: кубический корень из 19 683
Берём величину тысяч (19) и смотрим, между какими числами она находится (8 и 27). Соответственно, первой цифрой в ответе будет 2, а ответ лежит в диапазоне 20+.
Каждая цифра от 0 до 9 появляется в таблице по одному разу в виде последней цифры куба.
Так как последняя цифра в задаче — 3 (19 683), это соответствует 343 = 7^3. Следовательно, последняя цифра ответа — 7.
Ответ — 27.
Примечание: трюк работает только тогда, когда исходное число является кубом целого числа.
